KMP算法 | Tie × Wiki

kmp算法思想.png

一、KMP算法简介

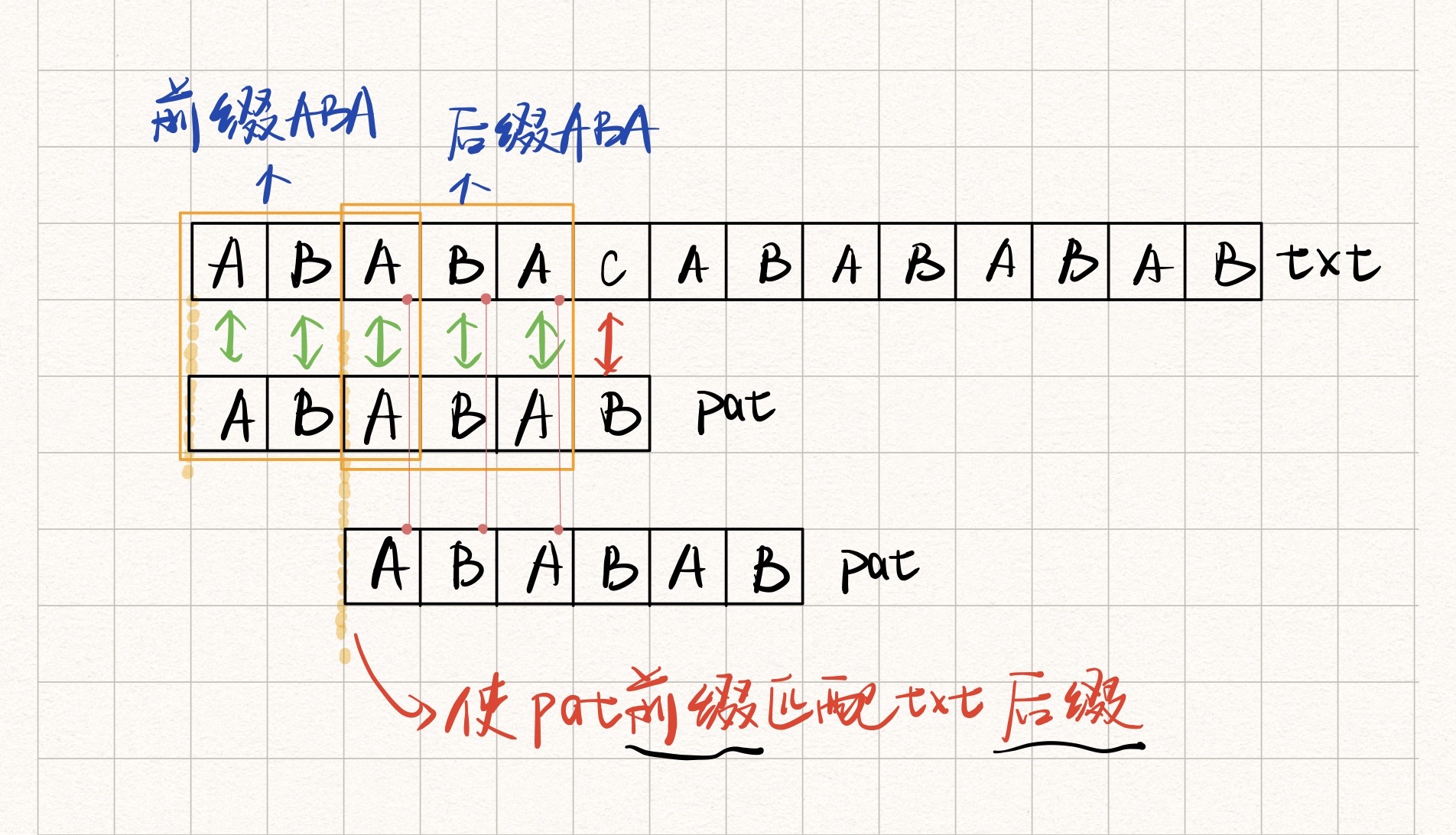
当目标串txt与模式串pat进行匹配时，如果txt[i]遇到不匹配的pat[j]时，不必像暴力匹配法那样每次只将pat后移一位，然后又从其第一位和txt[i+1]进行比较。

因为如果pat[0]~pat[j-1]有公共前后缀的话，那么txt[i]前的子串也必定存在一个公共前后缀

那么，我们可以将pat右移，使得从 pat的前缀匹配txt子串的前缀，pat的后缀匹配txt子串的后缀 ，变为pat的前缀匹配txt的后缀，这样就不必每次都移动一位，然后重新开始匹配

上面提到的公共前后缀，应该为最长公共前后缀，因为公共前后缀越短，移动的越多，就有可能漏掉部分匹配，导致结果的出错。
ababab的前缀为{‘a’,’ab’,’aba’,’abab’,’ababa’}，后缀为{‘b’,’ab’,’bab’,’abab’,’babab’}（不能是字符串本身）
它的最长公共字符串即为‘abab’.长度为4

二、PMT

PMT即 partial match table(部分匹配表)，当前子串（pat[0]~pat[j]）的最长公共前后缀
例如“ababab”

char	a	b	a	b	a	b
index	0	1	2	3	4	5
pmt	0	0	1	2	3	4

public static int[] getPMT(String s0) {
        char[] s = s0.toCharArray();
        int[] pmt = new int[s.length];

        for (int flag = 0, i = 1; i < s.length; ) {
            if (s[flag] != s[i] && flag == 0) { //如果s[i]和字符串的第一个不相同
                pmt[i] = 0;
                i++;
            } else if (s[flag] == s[i]) {   //如果s[i]相匹配，pmt[i]为其pmt[j]+1 （j<i）
                pmt[i] = flag + 1;
                i++;
                flag++;
            } else if (s[flag] != s[i] && flag != 0) { //如果不匹配且flag也不为0，则将最长公共前后缀缩小一个范围
                flag = pmt[flag - 1];
            }
        }

        return pmt;
    }

三、Next数组

在当前字符pat[j]之前的子串(pat[0]~pat[j-1])的最长公共前后缀，那么我们可以将PMT数组整体右移一位且Next[0]设为-1即可得到。

例如“ababab”

char	a	b	a	b	a	b
index	0	1	2	3	4	5
pmt	0	0	1	2	3	4
next	-1	0	0	1	2	3

3.1如何求next数组

递归得到

令next[0]=-1
如果当前位置元素s[i]的值与当前子串的最长公共前后缀（长度为K）的下一个元素s[k]相等，则最长公共前后缀长度加1，此时橙色长度+1（蓝色/绿色长度）作为s[i+1]的next值

如果不相等，则next值势必会缩小，由于长度为k的前缀、后缀（橙色部分）元素相同其相对位置也相同，那么他们各自的最长公共前后缀（朱红色）也势必相同。
如此，那么如果s[i]与 k缩小后的k`的下一个元素s[k`] 相等，那么m(s[i])就可以和n连起来了成为最长公共前后缀。
所以依次缩小k的范围，直至匹配

如果遇到next[k]=-1,则表名已经到了最后一个元素，,则表示无公共前后缀,停止匹配,next值为0
kmp(s[i]!=s[i]).jpg

public static int[] getNext(String s0) {
    char[] s = s0.toCharArray();
    int[] next = new int[s.length];

    // 初始条件
    int i = 0;
    int k = -1;
    next[0] = -1;

    // 根据已知的前i位推测第i+1位
    while (i < s.length - 1)  // 0 ~ i-2，next[i-1]是推出来的
    {
        //如果k=-1,则表示无公共前后缀，next值为0（-1++）
        //如果当前值和前一位的最大公共前后缀的下一位相等  例：如果s[i]=s[0] 则首位相等，next值：0+1=1
        if (k == -1 || s[i] == s[k]) {
            //k(之前的最长公共前后缀长度)+1 赋给 next[i+1] 
            //(因为s[i]和前面的在一起，作为s[i+1]的子串的长公共前后缀长度即next[i+1])
            next[++i] = ++k; 
        } else //不能匹配上
        {
            k = next[k];    //将k由 （0~S）的最长前后缀 改为  （0~S）的最长前后缀的最长前后缀
        }
    }
    return next;
}

四、KMP算法

如果txt[i]和pat[j]不匹配，则将txt[i]与pat[next[j]]进行匹配

设next[j]的长度为length,则pat[length]为最长公共前后缀的下一个元素
之前的元素pat[0]~pat[length-1] (一共length个元素)依然和之前的txt的后缀相匹配。

package array;

/**
 * Description
 * Author cloudr
 * Date 2020/7/20 23:13
 * Version 1.0
 **/
public class KMP {
    public static void main(String[] args) {
        String haystack = "mississippi";
        String needle = "issip";
        System.out.println(KMPByNext(haystack, needle));
    }

    public static int KMPByNext(String txt, String pat) {
        if (pat.length() == 0) return 0;
        int[] next = getNext(pat);
        int i = 0, j = 0;
        while (i < txt.length() && j < pat.length()) {
            //next值为-1，txt右移动一位,pat移动整个长度（j++=0）
            //如果匹配成功,继续将txt,pat的下一个元素进行匹配
            if (j == -1 || txt.charAt(i) == pat.charAt(j)) {
                i++;
                j++;
            } else //匹配失败则回溯
                j = next[j];
        }
        if (j == pat.length())
            return i - j;
        else
            return -1;
    }

    public static int[] getNext(String ps) {
        char[] strKey = ps.toCharArray();
        int[] next = new int[strKey.length];

        // 初始条件
        int i = 0;
        int k = -1;
        next[0] = -1;

        // 根据已知的前i位推测第j+1位
        while (i < strKey.length - 1)  // 0~ i-2 因为要整体右移一位且0位置为-1
        {
            //如果k=-1,则表示无公共前后缀，next值为0
            //如果当前值和前一位的最大公共前后缀的下一位相等  例：如果s[i]=s[0] 则首位相等，next值：0+1=1
            if (k == -1 || strKey[i] == strKey[k]) {
                next[++i] = ++k;    //k(之前的最长公共前后缀)+1 赋给 next[i+1] (因为next数组整体右移动一位)
            } else //不能匹配上
            {
                k = next[k];    //将k由 （0~S）的最长前后缀 改为  （0~S）的最长前后缀的最长前后缀
            }
        }
        return next;
    }
}

改进next数组

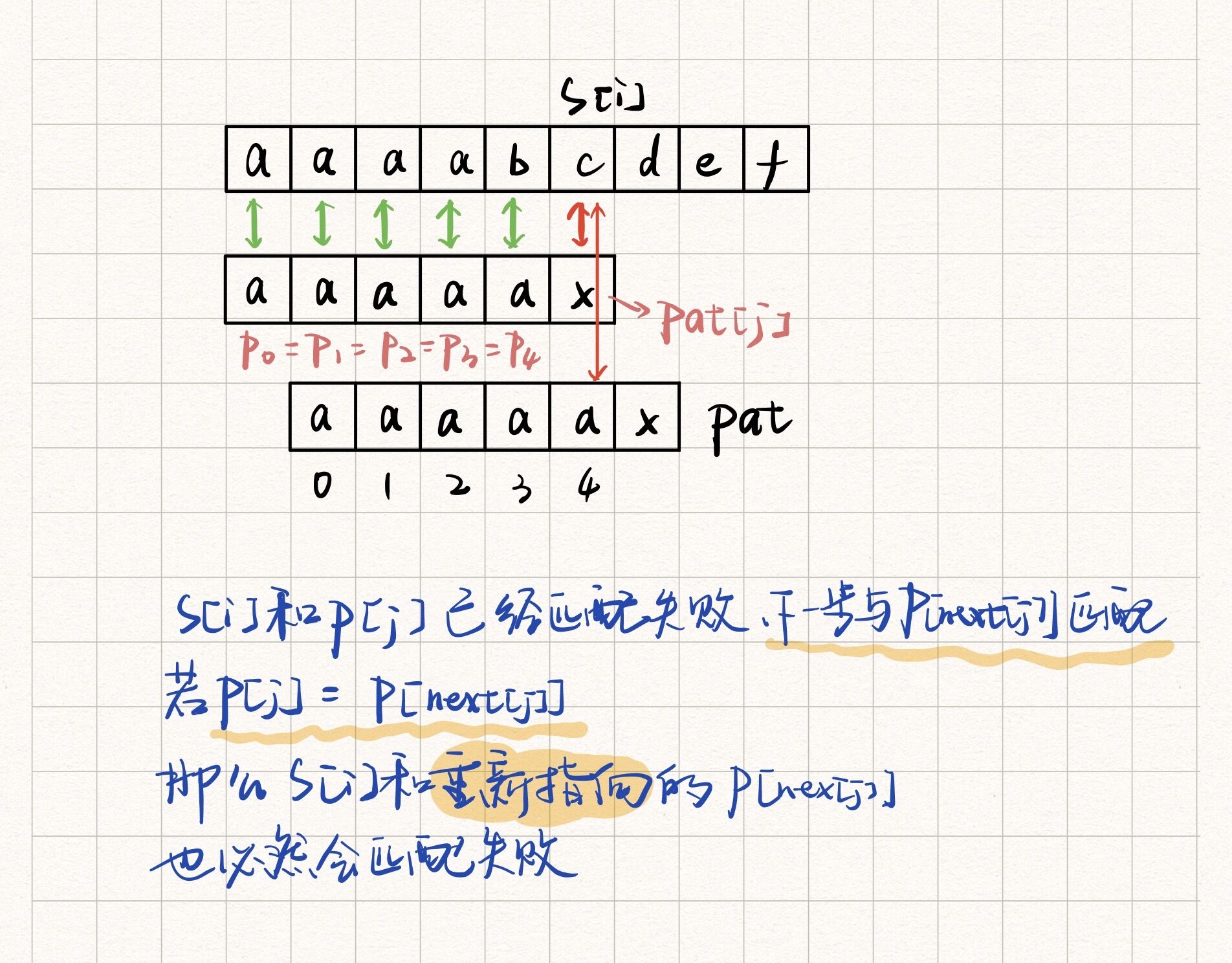
有txt=”aaaabcdef”，pat=”aaaaax”

next数组改进.jpg

s[i]和p[j]已经匹配失败，下一步会与p[ next[j] ]相匹配，但是如果p[j] == p[ next[j] ],那么后面s[i]和p[ next[j] ]的匹配也必然会失败，所以我们将p[ next[j] ]之前的子串的最长公共前后缀 next[ next[j] ]赋值给next[j]

public static int[] getNext(String s0) {
    char[] strKey = ps.toCharArray();
    int[] next = new int[strKey.length];

    // 初始条件
    int i = 0;
    int k = -1;
    next[0] = -1;

    // 根据已知的前i位推测第j+1位
    while (i < strKey.length - 1)  // 0~ i-2 因为要整体右移一位且0位置为-1
    {
        //如果k=-1,则表示无公共前后缀，next值为0
        //如果当前值和前一位的最大公共前后缀的下一位相等  例：如果s[i]=s[0] 则首位相等，next值：0+1=1
        if (k == -1 || strKey[i] == strKey[k]) {
            i++;    //赋给 next[i+1] (因为next数组整体右移动一位)
            k++;    //k(之前的最长公共前后缀)+1
            if (strKey[i] != strKey[k]) {
                next[i] = k;
            }
            else {  //不能出现p[j] = p[ next[j] ]的情况，如果出现，则将next[j]的范围缩小
                next[i] = next[k];      //  长度为k的pat[0]~pat[k-1]缩小一个范围 长度即为next[k]  k=next[i] , 则next[i] = next[k] = next [ next[i] ]
            }
        } else //不能匹配上
        {
            k = next[k];    //将k由 （0~S）的最长前后缀 改为  （0~S）的最长前后缀的最长前后缀
        }

    }
    return next;
}

~~基于PMT数组(未成功，对于某些子串符匹配会陷入死循环，待填坑)~~

String haystack = “mississippi”;
String needle = “issip”;

class Solution {
    public int strStr(String haystack, String needle) {
       if (needle.length() == 0) return 0;
        int[] pmt = getPMT(needle);
        int i = 0, j = 0;
        while (i < haystack.length() && j < needle.length()) {
            if (j == 0 && haystack.charAt(i) != needle.charAt(j)) {
                i++;
                if (i == haystack.length())
                    break;
            }

            if (haystack.charAt(i) == needle.charAt(j)) {

                i++;
                j++;
            } else
                j = j - pmt[j];
        }
        if (j == needle.length())
            return i - j;
        else
            return -1;
    }
}